Hoe vaak gebeurt het dat de oudste Belg overlijdt?

We zijn allemaal ooit de jongste mens op aarde geweest. Maar na zo’n kwartseconde waren we de titel van ‘jongste mens ter wereld’ naar verwachting alweer kwijt. Niemand die verder nog wakker ligt van dergelijke records. Anders is dat wanneer de oudste Belg/mens/man/vrouw/… komt te overlijden. Vorige week stonden de kranten er alweer vol van.

Via De Standaard vernamen we het trieste nieuws dat de oudste Belgische vrouw overleden is op 110 jarige leeftijd. Via Knack werden we verder ook nog ingelicht dat per toeval in dezelfde week ook de oudste vrouw ter wereld overleden is op 116 jarige leeftijd. Uit het artikel leren we ook nog dat deze laatste slechts 6 dagen de titel van oudste vrouw ter wereld gedragen heeft nadat op 1 april jl. een 117 jarige Japanse het leven liet.

Het verbaast me telkens hierover nieuwsberichten te lezen in onze (kwaliteits)media. Immers, per definitie is de oudste mens ter wereld erg oud en is de kans bijgevolg erg groot dat deze persoon over korte tijd zal overlijden. En telkens weer worden daar dan artikels over geschreven met bijhorende tips voor een lang leven.

Interessanter leek me de vraag hoe vaak we kunnen verwachten dat de oudste Belg komt te overlijden. En dat is een leuke analyse geworden (wie enkel het resultaat wil weten en niet de analyse zelf kan naar de laatste paragraaf scrollen).

De gegevens om dit te analyseren haalde ik van StatBel (vroegere Nationaal Instituut voor Statistiek). Daar kon ik zogenaamde ‘sterftetabellen’ downloaden.

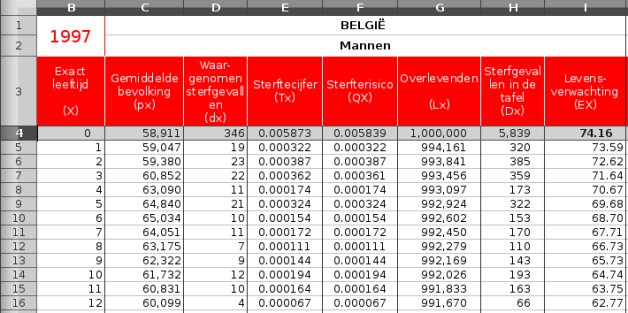In sterftetabellen staan een aantal statistieken, zoals het aantal inwoners voor elke leeftijd, de kans om te overlijden op elke leeftijd, levensverwachting, enz. Op basis van deze gegevens kunnen we ook een zogenaamde ‘overlevingscurve’ plotten.

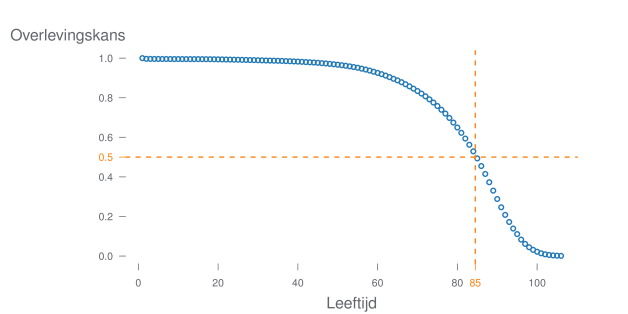Deze curve geeft voor elke leeftijd weer wat de kans is om minstens die leeftijd te bereiken. Bijvoorbeeld, in Belgie in 2013 is de kans om 85 of ouder te worden ongeveer 50%. Een curve die gerelateerd is aan de overlevingscurve is de risicocurve. Die curve geeft weer wat voor elke leeftijd de kans is te overlijden op die leeftijd.

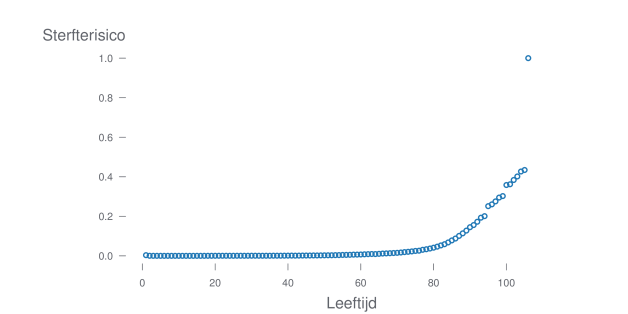Deze informatie zal ik nodig hebben voor de berekeningen. Maar, zoals je kan zien in de grafieken houdt StatBel enkel gegevens bij tot 105 jaar. Om ons probleem te kunnen oplossen hebben we echter gegevens nodig voor elke leeftijd tot ongeveer 122 jaar (de leeftijd van de oudste mens ter wereld ooit). We moeten de risicocurve dus op een of andere manier gaan extrapoleren. Dit heb ik gedaan door een machtsfunctie te schatten op de data (zie oranje lijn op figuur hieronder).

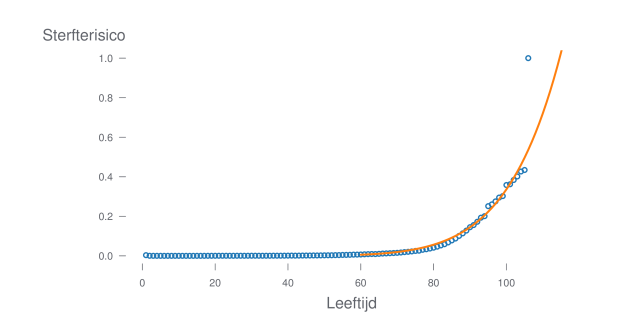Op die manier heb ik voor elke mogelijke leeftijd een inschatting van het risico te overlijden op die leeftijd. Merk op dat voor leeftijden waar het geschatte risico groter dan 1 was, ik dit afgerond heb naar 1 (gebeurde vanaf 115 jaar, wat ouder is dan de oudste Belg ooit, i.e. 112).

Tenslotte heb ik nog het aantal Belgen per leeftijdsgroep nodig. Immers, je kan je voorstellen dat wanneer er veel kinderen en weinig bejaarden zijn dit zorgt dat de titel van ‘oudste inwoner’ minder snel afgelost zal worden. Deze data kan gemakkelijk uit de sterftetabellen gehaald worden. Echter, opnieuw worden alle mensen ouder dan 104 in dezelfde categorie onder gebracht. Dus moet er ook een schatting gemaakt worden van hoe die (74 gevallen) verdeeld zijn over de leeftijden 105 tot 110 (leeftijd huidige oudste Belg). Om dit te doen heb ik het cummulatieve product van de geschatte risicocurve berekend en dit gebruikt als kansen in een multinomiale verdeling.

Om de eigenlijke simulatie te kunnen doen moest ik een aantal assumpties maken. De belangrijkste is ongetwijfeld dat ik er van uit gegaan ben dat de risicocurve niet zal veranderen in de komende 10 jaar (en dat de staart ervan met een machtsfunctie beschreven kan worden). Wellicht is dit onrealistisch, maar door over een periode van slechts 10 jaar te simuleren hoop ik hieraan toch wat tegemoet te komen. Verder ben ik er ook van uit gegaan dat het risico om te overlijden binnen een bepaald jaar (dus elke dag van dat jaar) even groot is. Merk op dat deze assumpties ervoor zorgen dat de resultaten met de nodige kritische zin moeten worden bekeken.

In woorden werkt het simulatie algoritme ongeveer als volgt:

• Voor elke leeftijd, simuleer het aantal overlijdens adhv een binomiaalverdeling met n gelijk aan het aantal Belgen in die leeftijdscategorie en p gelijk aan het risico voor die leeftijd.
• Ga na of de oudste Belg overleden is (dit is gecompliceerder dan op het eerste zicht lijkt wegens mogelijk meerdere overlijdens van oudste Belgen binnen hetzelfde jaar).
• Indien ja, tel het aantal oudste Belgen die zijn overleden binnen datzelfde jaar. Simuleer hiervoor de sterfdagen uit de uniforme verdeling U[0,365].
• Vermeerder de leeftijd van alle niet overleden Belgen met 1.
• Simuleer het aantal geboortes (leeftijd 0). Hiervoor gebruikte ik het geboortecijfer van 2012 (i.e. ongeveer 126.000)
• Indien 10 jaar gesimuleerd, schrijf resultaten weg en begin opnieuw.
• Herhaal dit proces vele keren (i.e. 10.000 keer).

Onderstaande grafiek geeft het resultaat weer van 10.000 simulaties van overlijdens voor het komende decennium in België. Je ziet hoe vaak we kunnen verwachten dat de ‘oudste Belg’ zal komen te overlijden per jaar.

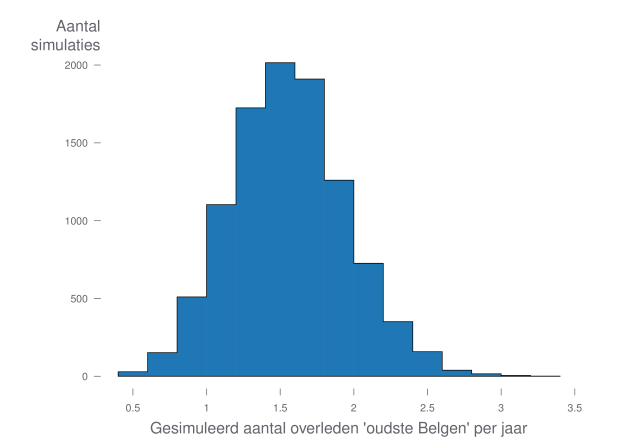De waarde 1,5 is het meest waarschijnlijk. Dit betekent dat we kunnen verwachten dat we in het komende decennium ongeveer 1,5 keer per jaar (anders gezegd, 1 à 2 keer per jaar) in de krant te zullen lezen dat de oudste Belg is overleden. Als de kranten zich hiernaast ook nog interesseren voor ‘de oudste mannelijke Belg’ en ‘de oudste vrouwelijke Belg’ en ‘de oudste wereldburger’ enzovoort, dan mogen we ons aan een veelvoud van dergelijke artikelen verwachten. JOY!

Als toemaatje heb ik ook nog berekend wat de kans is dat het leeftijdsrecord van de oudste Belg ooit (112) overschreden zal worden het komende decennium. Het blijkt dat die kans ongeveer 28% bedraagt en indien dit inderdaad zou gebeuren dan mogen we verwachten dat deze heugelijke gebeurtenis zich binnen ongeveer 6.5 jaar zal voordoen.

Afspraak binnen 10 jaar voor mijn evaluatie…

Kleine gemeente, fijne gemeente? Over “het gemeenterapport” van Het Nieuwsblad.

Intro

De voorbije week presenteerde Het Nieuwsblad elke dag een reportage over ‘Het Gemeenterapport‘, een grootschalige enquête die het dagblad, in samenwerking met onderzoeksbureau iVox, afnam van meer dan 116.000 Vlamingen. De vragen gingen over diverse lokale thema’s maar ook over het nieuwe gemeentebestuur.

De eerste reportage ging over in welke gemeenten we het liefste wonen. In de vragenlijst werd aan de 116.000 Vlamingen gevraagd om te antwoorden met een score tussen 0 en 10 op de volgende vraag: ‘Hoe graag woont u in uw gemeente?‘. Hieronder de resultaten zoals ze gepresenteerd werden door Het Nieuwsblad (eigen reproductie obv de beschikbare gegevens):

Op de kaart van Vlaanderen is elke gemeente in een kleur weergegeven dat overeenkomt met de gemiddelde score van die gemeente. In de inleiding van het artikel schrijft Het Nieuwsblad:

Inwoners van Linkebeek, Vorselaar en Zutendaal wonen het liefst in hun gemeente. Tienen, Vilvoorde en Zelzate scoren dan weer het slechtst. Dat blijkt uit Het Gemeenterapport van Het Nieuwsblad.
Het Nieuwsblad – 20/01/2014

Op twitter werd er duchtig gereageerd op Het Gemeenterappport. Een tweet die me opviel kwam van Bert Kruismans (@kruismans) die de score van een gemeente (Linkebeek) ging linken aan een kenmerk van die gemeente (faciliteitengemeente):

De fijnste gemeente van Vlaanderen is een faciliteitengemeente. http://t.co/aZx7IUJoQA via @nieuwsblad_be

— Bert Kruismans (@kruismans) January 21, 2014

In deze blogpost wil ik graag verduidelijken waarom dergelijke conclusies voorbarig zijn.

Steekproef

Een vragenlijst die werd afgenomen bij meer dan 116.000 Vlamingen lijkt heel erg betrouwbaar te zijn. De steekproef is in elk geval gigantisch groot. En zolang we op basis van die vragenlijst enkel conclusies trekken over ‘dé Vlamingen’ is er ook geen enkel probleem.

Echter, de bedoeling van Het Gemeenterapport is niet om over de Vlaming in het algemeen te rapporteren, maar wel om de resultaten te gaan vergelijken over de verschillende gemeenten heen. En dan is het niet de totale steekproefgrootte die van belang is, maar de steekproefgroottes voor elke gemeente afzonderlijk. Volgend fictief voorbeeldje kan dit helpen verduidelijken:

Men wil de tevredenheid van de inwoners in twee steden, Gent en Kortrijk, met elkaar vergelijken. Om dit te onderzoeken is er een budget voorzien om 1000 inwoners te bevragen. Aan elke inwoner wordt gevraagd hoe fijn ze hun stad vinden (score op 10). Stel nu dat een (naïve) onderzoeker beslist om slechts 2 vragenlijsten af te nemen in Kortrijk en overige 998 in Gent.

Uit het onderzoek blijkt dat de gemiddelde score voor Kortrijk 6/10 is, terwijl de gemiddelde score voor Gent 7,5/10 is. Is het zinvol om te besluiten dat het zoveel fijner wonen is in Gent?

Het is duidelijk dat men dit niet zomaar kan besluiten. Een totaal van 1000 enquêtes is best veel, maar aangezien er slechts 2 in Kortrijk werden afgenomen is deze meting veel minder betrouwbaar dan de meting in Gent.

De kern van het probleem zou hiermee duidelijk moeten zijn: de gemiddelde tevredenheidsscores zoals ze op bovenstaand kaartje zijn weergegeven kunnen moeilijk geïnterpreteerd worden zonder informatie over hoe betrouwbaar elke score is.

‘Kleine gemeenten probleem’

Een probleem dat hieruit voortvloeit, is dat (in dit geval) gemeenten waar men slechts een kleine steekproef heeft genomen een veel grotere kans hebben om extreme uitkomsten te genereren. Hoe kleiner de steekproef, hoe groter de kans op extremen. (voor voorbeelden uit de gezondheidszorg, zie referentie onderaan deze blogpost)

Een veelgemaakte fout is dat een steekproef groter moet zijn voor grotere gemeentes (en omgekeerd) wanneer men gemeenten wil gaan vergelijken. Of, wat op hetzelfde neerkomt, dat elke inwoner van Vlaanderen dezelfde kans moet hebben om in de steekproef te belanden (wanneer men gemeenten wil gaan vergelijken). Onderstaande analyse geeft weer wat dan gebeurt:

Stel dat in elke Vlaamse gemeente de ‘echte’ tevredenheid exact dezelfde is, namelijk 7,25/10 (en dat 95% van de inwoners van elke gemeente zijn/haar gemeente een score tussen 5 en 9,5 zou geven).

Aangezien deze ‘echte’ tevredenheid niet gekend is, doet men een grootschalig onderzoek. Er is een groot budget beschikbaar waarmee het mogelijk is om 116.000 vragenlijsten af te nemen.

Elke inwoner van een Vlaamse gemeente heeft dezelfde kans om in de steekproef te worden opgenomen, dwz omdat Gent 3,3x meer inwoners heeft dan Kortrijk, worden ook 3,3x meer Gentenaars dan Kortrijkzanen in de steekproef opgenomen.

Hieronder een animatie van hoe 100 verschillende resulterende kaartjes er zouden kunnen uitzien (2 per seconde):

Merk op dat alle gemeentes eigenlijk oranje zouden moeten zijn (want de ‘echte’ tevredenheid bedraagt 7,25/10 voor elke gemeente). Echter, de animatie toont dat er toch steeds enkele gemeentes zijn die beter of slechter scoorden dan de rest (oa vaak Linkebeek). Dit betekent echter niet dat inwoners van die gemeentes meer of minder tevreden zijn dan de zij in andere gemeentes. Het is de kleine steekproef in die gemeenten die zorgt voor de grotere kans op extreme observaties.

Conclusie

Het kaartje, zoals het gepubliceerd werd op de website van Het Nieuwsblad, geeft te weinig informatie om de analyse ten gronde te kunnen voeren. Linkebeek, Vorselaar en Zutendaal halen inderdaad de hoogste scores, maar het zijn ook stuk voor stuk kleine gemeentes. Zonder extra informatie is het erg moeilijk om in te schatten of deze gemeentes ‘extreem’ scoren wegens bovenstaand steekproefprobleem of omdat het daar echt zo fijn wonen is.

Het is des mensen om altijd en overal oorzakelijke verbanden te gaan zoeken/zien bij opmerkelijke waarnemingen. Zeker journalisten, opiniemakers, experten allerhande hebben deze neiging. En dat is een goeie zaak, want het is ook hun taak om dingen in perspectief te plaatsen. Maar het wordt problematisch wanneer men toevallige fluctuaties gaat gaan verklaren. Data-journalist Maarten Lambrechts (@maartenzam) had alvast de goede reflex:

Lokale datajournalistiek van @Nieuwsblad_be http://t.co/iLkOiYr1tD Enig zicht op betrouwbaarheidsintervallen, @stevendegrove?

— Maarten Lambrechts (@maartenzam) January 20, 2014

Jammer dat er geen antwoord op deze terechte vraag is gekomen…

Een meer formele en uitgebreide bespreking van bovenstaande ideeën kan in de paper ‘Gelman – All maps of parameter estimates are misleading‘ gevonden worden.

R: Create plots in your university or company colors

PowerPoint (or Beamer) presentations look so much better if the colors of the slide headers somewhat match the colors of the text and figures. Many of the plots that I make, are created with R.  I find it easy to have the colors of my university (Ghent University) available in R. Below some simple slides made with the great UGent Beamer extension.

The rgb() function in the grDevices package makes it very easy to define new colors. If you want to add your own university of company colors, you just need to know the red-green-blue codes of the colors you want to add.

If you don’t know the RGB values of the colors you want to add, you can just open your logo in MS Paint (or similar) and use the color-pick tool. This will give you the required RGB values. Below an example of the color-pick tool in KolourPaint.

Finally, to make your new colors available when R starts up, just define the new colors in your Rprofile file. Just make sure that you FIRST load the grDevices library or an error will occur. For example, if you want to use the Ghent University colors, just add the following lines to your Rprofile:

library("grDevices")
# Pantone 534: global
ugentblue <- rgb(36,71,127,maxColorValue=250)
# Pantone 130: generic colour
ugentyellow <- rgb(250,178,10,maxColorValue=250)
# Pantone 103c: Faculty of Literature & Philosophy
ugent_lw <- rgb(214,198,0,maxColorValue=250)
# Pantone 485c: Faculty of Law
ugent_re <- rgb(238,39,34,maxColorValue=250)
# Pantone 292c: Faculty of Science
ugent_we <- rgb(131,194,236,maxColorValue=250)
# Pantone 702: Faculty of Medicine and Health Sciences
ugent_ge <- rgb(232,80,118,maxColorValue=250)
# Pantone 272c: Faculty of Engineering and Architecture
ugent_tw <- rgb(116,121,197,maxColorValue=250)
# Pantone 556c: Faculty of Economics and Business Administration
ugent_eb <- rgb(113,165,136,maxColorValue=250)
# Pantone 2583c: Faculty of Veterinary Medicine
ugent_di <- rgb(145,94,182,maxColorValue=250)
# Pantone 1655c: Faculty of Psychology and Educational Sciences
ugent_pp <- rgb(244,106,37,maxColorValue=250)
# Pantone 3262c: Faculty of Bioscience Engineering
ugent_la <- rgb(74,194,182,maxColorValue=250)
# Pantone purple: Faculty of Pharmaceutical Sciences
ugent_fw <- rgb(163,43,155,maxColorValue=250)
# Pantone 375c: Faculty of Political and Social Sciences
ugent_ps <- rgb(159,217,93,maxColorValue=250)